Apuntes de Teoría de grafos y árboles

TEORÍA DE GRAFOS Y ARBOLES

La teoría de grafos.

También llamada teoría de gráficas, es una rama de las matemáticas y las ciencias de la computación que estudia las propiedades de los grafos, Los grafos no deben ser confundidos con las gráficas, que es un término muy amplio.
Los grafos son estructuras discretas compuestas por vértices y aristas que conectan pares de esos puntos.

Entre las aplicaciones de la Teoría de gráficas que se han vuelto importantes:

el estudio de las redes sociales, comunicaciones, tomar datos de resonancia magnética del cerebro y muchísimas mas.

composición de un grafo:

Aristas: Son las líneas con las que se unen los vértices de un grafo.
- Aristas adyacentes: 2 aristas son adyacentes si convergen en el mismo vértice.
- Aristas paralelas: Son dos aristas conjuntas si el vértice inicial y final son el mismo.
- Arista cíclicas: Es la arista que parte de un vértice para entrar en sí mismo.
- Cruce: Son 2 aristas que cruzan en un mismo punto.

Vértices: Los vértices son los elementos que forman un grafo. Cada uno lleva asociada una valencia característica según la situación, que se corresponde con la cantidad de aristas que confluyen en dicho vértice.

Camino: Se denomina camino de un grafo a un conjunto de vértices interconectados por aristas. Dos vértices están conectados si hay un camino entre ellos.

Tipos de grafos

Grafo simple: O simplemente grafo es aquel que acepta una sola arista uniendo dos vértices cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única que une dos vértices específicos. Es la definición estándar de un graf.

Multigrafo: o pseudografo: Es el que acepta más de una arista entre dos vértices. Estas aristas se llaman múltiples o lazos (loops en inglés). Los grafos simples son una subclase de esta categoría de grafos. También se les llama grafos general.

Resultado de imagen para grafo multigrafo

Grafo orientado: grafo dirigido o digrafo. Son grafos en los cuales se ha añadido una orientación a las aristas, representada gráficamente por una flecha.

Resultado de imagen para grafo orientado

Grafo etiquetado: Grafos en los cuales se ha añadido un peso a las aristas (número entero generalmente) o un etiquetado a los vértices.

Resultado de imagen para grafo etiquetado

Grafo aleatorio: Grafo cuyas aristas están asociadas a una probabilidad.

Resultado de imagen para grafo aleatorio

Hipergrafo: Grafos en los cuales las aristas tienen más de dos extremos, es decir, las aristas son incidentes a 3 o más vértices.

Grafo infinito: Grafos con conjunto de vértices y aristas de cardinal infinito.

Grafo plano: Los grafos planos son aquellos cuyos vértices y aristas pueden ser representados sin ninguna intersección entre ellos. Podemos establecer que un grafo es plano gracias al Teorema de Kuratowskiz

Resultado de imagen para tipos de grafos

Arboles
Un árbol se define como un tipo de grafo que no contiene ciclos, es decir es un grafo también acíclico, pero a su vez es conexo. Tal es el caso de los siguientes dos grafos en donde se puede notar que ninguno de los dos contiene repeticiones (ciclos).

Un árbol es un grafo simple no dirigido G que satisface:

G es conexo y no tiene ciclos .
G no tiene ciclos y, si se añade alguna arista se forma un ciclo.
G es conexo y si se le quita alguna arista deja de ser conexo.
G es conexo y el grafo completo de 3 vértices $K_{3}$ no es un menor de G.
Dos vértices cualquiera de G están conectados por un único camino simple.

Todo árbol es a su vez un grafo con sólo un conjunto numerable de vértices es además un grafo plano.

Todo grafo conexo G admite un árbol de expansión, que es un árbol que contiene cada vértice de G y cuyas aristas son aristas de G.

Ejemplos de arboles

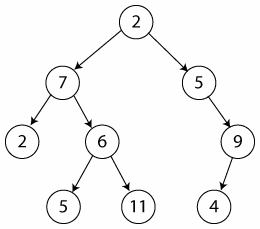
Este grafo representa un árbol binario completo porque cada uno de sus vértices internos tiene un hijo.

En esta figura se representa un árbol, árbol 3-ario, completo porque cada uno de sus vértices internos tiene tres hijos.

Este es un árbol 5-ario completo porque cada vértice interno tiene 5 hijos.

Este grafo representa un árbol m-ario completo para alguna m, porque algunos de sus vértices internos tienen dos hijos y otros tienen tres hijos.

Árboles de decisión

Los árboles con raíz pueden ser empleados para modelar problemas en los que una serie de decisiones conducen a la solución:

Árboles binarios

Definición: un árbol binario es un árbol con raíz en el cual cada vértice tiene cero, uno o dos hijos. Si un vértice tiene un hijo, ese hijo se designa como un hijo izquierdo o un hijo derecho (pero no ambos). Si un vértice tiene dos hijos, uno de ellos se designa como un hijo izquierdo y el otro se designa como un hijo derecho.

Pasos para realizar el algoritmo:

1. Se marca un nodo cualquiera, será el nodo de partida.
2. Seleccionamos la arista de menos valor incidente en el nodo marcado anteriormente, y marcamos el otro nodo en el que incide.
3. Repetir el paso 2 siempre que la arista elegida enlace un nodo y otro que no lo esté.
4. El proceso termina cuando tenemos todos los nodos del grafo marcados.

Al concluir el algoritmo, T es un árbol de expansión mínimo.

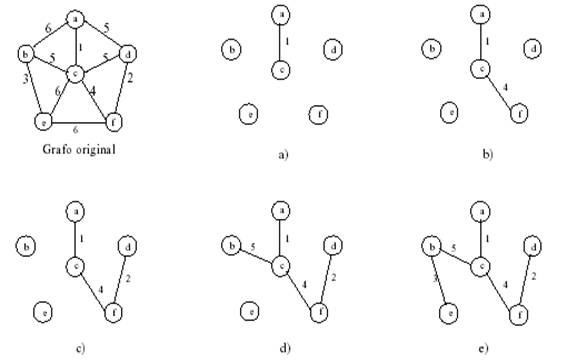
Algoritmo de Kruskal: Se eligen aristas de la forma más económica. Inicialmente se ordenan las aristas por su peso. A continuación se van eligiendo las aristas de menor peso de modo tal, que no formen ciclo con las aristas anteriormente seleccionadas. Para evitar que se formen ciclos se asignan etiquetas a los vértices de modo que los vértices que formen parte de las aristas ya elegidas tengan todos la misma etiqueta. Una etiqueta es unainformación asociada a un vértice que los hace distinguibles entre sí.

1. T= {}

2. Asignar etiquetas a todos los vértices t(i)=i, i=1, 2, ..., n.

3. Mientras haya vértices con etiquetas diferentes repetir.

a) Escoger la arista (u, v) de menor peso tal que t(u) sea diferente de t(v). Agregarla a T

b) Asignar a todos los vértices de una componente conexa de T la misma etiqueta.